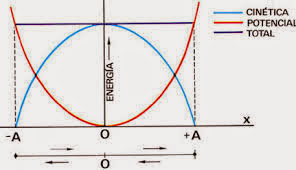
En el m.a.s. la energía se transforma continuamente de potencial en cinética y viceversa.
En los extremos solo hay energía potencial puesto que la velocidad es cero y en el punto de equilibrio solo hay energía cinética. En cualquier otro punto, la energía correspondiente a la partícula que realiza el m.a.s. es la suma de su energía potencial más su energía cinética.

Toda partícula sometida a un movimiento armónico simple posee una energía mecánica que podemos descomponer en: Energía Cinética (debida a que la partícula está en movimiento) y Energía Potencial (debida a que el movimiento armónico es producido por una fuerza conservativa).

Si tenemos en cuenta el valor de la energía cinética
Ec = 1/2 m v²
y el valor de la velocidad del m.a.s.
v = dx / dt  = A w cos (w t + j_o)
sustituyendo obtenemos
Ec  = 1/2 k A² cos ²(w t + j_o)
a partir de la ecuación fundamental de la trigonometría:

sen² + cos² = 1
Ec  = 1/2 k A² [ 1 - sen ²(w t + j_o)]
Ec  = 1/2 k[ A² - A²sen ²(w t + j_o)]

de donde la energía cinética de una partícula sometida a un m.a.s. queda
Ec  = 1/2 k [ A² - x²]

Observamos que tiene un valor periódico, obteniéndose su valor máximo cuando la partícula se encuentra en la posición de equilibrio, y obteniéndose su valor mínimo en el extremo de la trayectoria.

La energía potencial en una posición y vendrá dada por el trabajo necesario para llevar la partícula desde la posición de equilibrio hasta el punto de elongación y.
Por ello el valor de la energía potencial  en una posición x vendrá dado por la expresión
Ep = 1/2 k x²
Teniendo en cuenta que la energía mecánica es la suma de la energía potencial  más la energía cinética, nos encontramos que la energía mecánica de una partícula que describe un m.a.s. será:

E_total = 1/2 K x² +  1/2 K (A²-x²) = 1/2 KA²

E = 1/2 k A²

En el m.a.s. la energía mecánica permanece constante si no hay rozamiento, por ello su amplitud permanece también constante.