Realizado por: Joaquin Huauya A.

Movimiento Armónico Simple




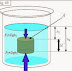
Es un movimiento periódico, oscilatorio y vibratorio en ausencia de fricción, producido por la acción de una fuerza recuperadora que es directamente proporcional a la posición pero en sentido opuesto.

  • Movimiento Armónico: sen, cos
  • Movimiento periódico complejo:admite soluciones armónicas.

Descripción del M.A.S:

a)Descripción Cinemática .

El movimiento armónico simple es un movimiento periódico de vaivén, en el que un cuerpo oscila de un lado al otro de su posición de equilibrio, en una dirección determinada, y en intervalos iguales de tiempo.
Por ejemplo, es el caso de un cuerpo colgado de un muelle oscilando arriba y abajo.El objeto oscila alrededor de la posición de equilibrio cuando se le separa de ella y se le deja en libertad. En este caso el cuerpo sube y baja.
Es también, el movimiento que realiza cada uno de los puntos de la cuerda de una guitarra cuando esta entra en vibración; pero, pongamos atención, no es el movimiento de la cuerda, sino el movimiento individual de cada uno de los puntos que podemos definir en la cuerda. El movimiento de la cuerda, un movimiento ondulatorio, es el resultado del movimiento global y simultáneo de todos los puntos de la cuerda. 

x(t) = A \cos(\omega t + \phi)\,

donde:
x\, es la elongación o desplazamiento respecto al punto de equilibrio.
A\, es la amplitud del movimiento (elongación máxima).
\omega\, es la frecuencia angular
t\, es el tiempo
\phi\, es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.

Además, la frecuencia de oscilación puede escribirse como esto:

f = \frac{\omega}{2 \pi} = \frac{1}{2 \pi} \sqrt{\frac{k}{m}}

Por lo que el periodo:

T = \frac{1}{f} = \frac{2 \pi}{\omega} = 2 \pi \sqrt{\frac{m}{k}}

b)Descripción Dinámica.

En el movimiento armónico simple la fuerza que actúa sobre el móvil es directamente proporcional: 

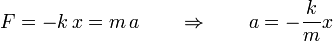
F=-k\, x=m\, a\qquad\Rightarrow\qquad a=-\frac{k}{m}x

Comparando esta ecuación y la que teníamos para la aceleración se deduce:

\omega^{2}=\frac{k}{m}

Esta ecuación nos permite expresar el periodo (T) del movimiento armónico simple en función de la masa de la partícula y de la constante elástica de la fuerza que actúa sobre ella:

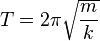
T = 2 \pi \sqrt{\frac{m}{k}}